Find max diameter of binary tree

20 March 2015

Problem overview

The max diameter of binary tree is the largest distance between 2 nodes in the tree.

Example:

    balanced binary tree

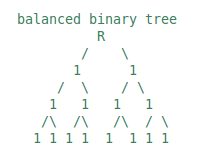
TEXT screenshot

Answer: 7

    unbalanced binary tree

TEXT screenshot

Answer: 9

Algorithm analysis

  1. The Max diameter of a balanced tree will always pass through root, and it will be the sum of the 2 biggest branches from root - 1 (to not count root twice).

  2. The Max diameter of an unbalanced tree might pass or not through root, for that it is necessary to sum and calculate the max diameter from each subtree from left or right and compare with current found max diameter (max height from left and right branches combined).

Code in Java

Node class:

class NodeB {



<span class="kt">int</span> <span class="n">val</span><span class="o">;</span>
<span class="n">NodeB</span> <span class="n">parent</span><span class="o">;</span>
<span class="n">NodeB</span> <span class="n">left</span><span class="o">,</span> <span class="n">right</span><span class="o">;</span>

<span class="n">NodeB</span><span class="o">(</span><span class="kt">int</span> <span class="n">val</span><span class="o">)</span> <span class="o">{</span>
    <span class="k">this</span><span class="o">.</span><span class="na">val</span> <span class="o">=</span> <span class="n">val</span><span class="o">;</span>
    <span class="k">this</span><span class="o">.</span><span class="na">left</span> <span class="o">=</span> <span class="kc">null</span><span class="o">;</span>
    <span class="k">this</span><span class="o">.</span><span class="na">right</span> <span class="o">=</span> <span class="kc">null</span><span class="o">;</span>
<span class="o">}</span>

<span class="n">NodeB</span><span class="o">(</span><span class="kt">int</span> <span class="n">val</span><span class="o">,</span> <span class="n">NodeB</span> <span class="n">left</span><span class="o">,</span> <span class="n">NodeB</span> <span class="n">right</span><span class="o">)</span> <span class="o">{</span>
    <span class="k">this</span><span class="o">.</span><span class="na">val</span> <span class="o">=</span> <span class="n">val</span><span class="o">;</span>
    <span class="k">this</span><span class="o">.</span><span class="na">right</span> <span class="o">=</span> <span class="n">right</span><span class="o">;</span>
    <span class="k">this</span><span class="o">.</span><span class="na">left</span> <span class="o">=</span> <span class="n">left</span><span class="o">;</span>
<span class="o">}</span>




}

diameter calculation:

    public int findMaxDiameterOfBinaryTree(NodeB root) {
        if (root == null) {
            return 0;
        }
        int heightLeft = findTreeHeight(root.left);
        int heightRight = findTreeHeight(root.right);



    <span class="k">return</span> <span class="n">Math</span><span class="o">.</span><span class="na">max</span><span class="o">((</span><span class="n">heightLeft</span> <span class="o">+</span> <span class="n">heightRight</span> <span class="o">+</span> <span class="mi">1</span><span class="o">),</span> 
            <span class="n">Math</span><span class="o">.</span><span class="na">max</span><span class="o">(</span><span class="n">findMaxDiameterOfBinaryTree</span><span class="o">(</span><span class="n">root</span><span class="o">.</span><span class="na">left</span><span class="o">),</span> <span class="n">findMaxDiameterOfBinaryTree</span><span class="o">(</span><span class="n">root</span><span class="o">.</span><span class="na">right</span><span class="o">)));</span>
<span class="o">}</span>

<span class="kd">public</span> <span class="kt">int</span> <span class="nf">findTreeHeight</span><span class="o">(</span><span class="n">NodeB</span> <span class="n">root</span><span class="o">)</span> <span class="o">{</span>
    <span class="k">if</span> <span class="o">(</span><span class="n">root</span> <span class="o">==</span> <span class="kc">null</span><span class="o">)</span> <span class="o">{</span>
        <span class="k">return</span> <span class="mi">0</span><span class="o">;</span>
    <span class="o">}</span>                        
    <span class="k">return</span> <span class="mi">1</span> <span class="o">+</span> <span class="n">Math</span><span class="o">.</span><span class="na">max</span><span class="o">(</span><span class="n">findTreeHeight</span><span class="o">(</span><span class="n">root</span><span class="o">.</span><span class="na">left</span><span class="o">),</span> <span class="n">findTreeHeight</span><span class="o">(</span><span class="n">root</span><span class="o">.</span><span class="na">right</span><span class="o">));</span>        
<span class="o">}</span></code></pre></figure>







Full source code
comments powered by Disqus